GENERATING THE LAZY CATERER'S SEQUENCE IN C++ LANGUAGE
AMRUHA AHMED
14th October,2023.
The lazy caterer's sequence provides you with a lucid way to calculate the maximum number of pieces of a disk shaped object which can be made using straight cuts.
The formula to generate this sequence is:
(n^2+n+2)/2 or simply nC0+nC1+nC2(if n>=2)
Where n represents the number of cuts made to the disk-like object.

In this blog post, I will be discussing about the generation of the lazy caterer's sequence using the formulae mentioned above.
METHOD-1
In this method, the formula of nC0+nC1+nC2 will be used to calculate the terms of the lazy caterer's sequence. The following things need to be kept in mind while following this approach:
- 1.When n=0, then the term of the sequence should not contain the values of nC1 and nC2 since 0C1 and 0C2 do not exist
- 2.When n=1, then the term of the sequence should not contain the value of nC2 since 1C2 does not exist.
VARIABLES REQUIRED:
- a-parameter to the fact()
- n-maximum number of cuts to be made
- term1-stores nC0
- term2-stores nC1
- term3-stores nC2
- i-loop counter
- finalterm-sum of term1,term2 and term3(substitution of formula)
FUNCTIONS REQUIRED:
- 1.main()-contains the steps required to calculate and display the numbers of sequence
- 2.fact()-recursive function to calculate the factorial of the parameter 'a'
ALGORITHM FOR THE MAIN FUNCTION:
- 1.Start
- 2. Accept the number of terms of the sequence to be generated in 'n'
- 3.Initialize term1, term2 and term3 to 0
- 4.Loop counter i is initialized to 0
- 5.While i is less than or equal to 'n' the following steps need to be repeated:
- (i)initialize finalterm to 0
- (ii)calculate term1(nC0) as fact(i)/fact(i-1)
- (iii) when i is not equal to 0 , execute the next statements otherwise make term2=0
- (iv) calculate term2(nC1) as fact(i)/(fact(i-1)*fact(1))
- (v)if i is not equal to 1 then move to the next step otherwise make term3 to 0
- (vi)calculate term3(nC2) as fact(i)/(fact(i-2)*fact(2))
- (vii)calculate finalterm as term1+term2+term3
- (viii)display finalterm
- 6.Stop
PROGRAM:
#include<iostream>
using namespace std;
int fact(int a)//function to calculate factorial
{
if(a==0)
return 1;
else
return(a*fact(a-1));
}
int main()
{
int n;
int i;
cout<<"Enter the maximum number of cuts to be made:";
cin>>n;
int term1=0,term2=0,term3=0; //term1 =nC0, term2 for nC1, term3 for nC2
cout<<"The lazy Caterer's Sequence is ...\n";
for(i=0;i<=n;i++)// i is the loop counter
{
int finalterm=0;//to store the sum of term1,term2 and term3(substitution of formula)
term1=fact(i)/(fact(i)*fact(0));
if(i!=0)
{
term2=fact(i)/(fact(i-1)*fact(1));
if(i!=1)
term3=fact(i)/(fact(i-2)*fact(2));
else
term3=0;
}
else
{
term2=0;
}
finalterm=term1+term2+term3;
cout<<finalterm<<"\t";
}
return 0;
}
DRY RUN:
if n=4 then the following steps are executed in the loop: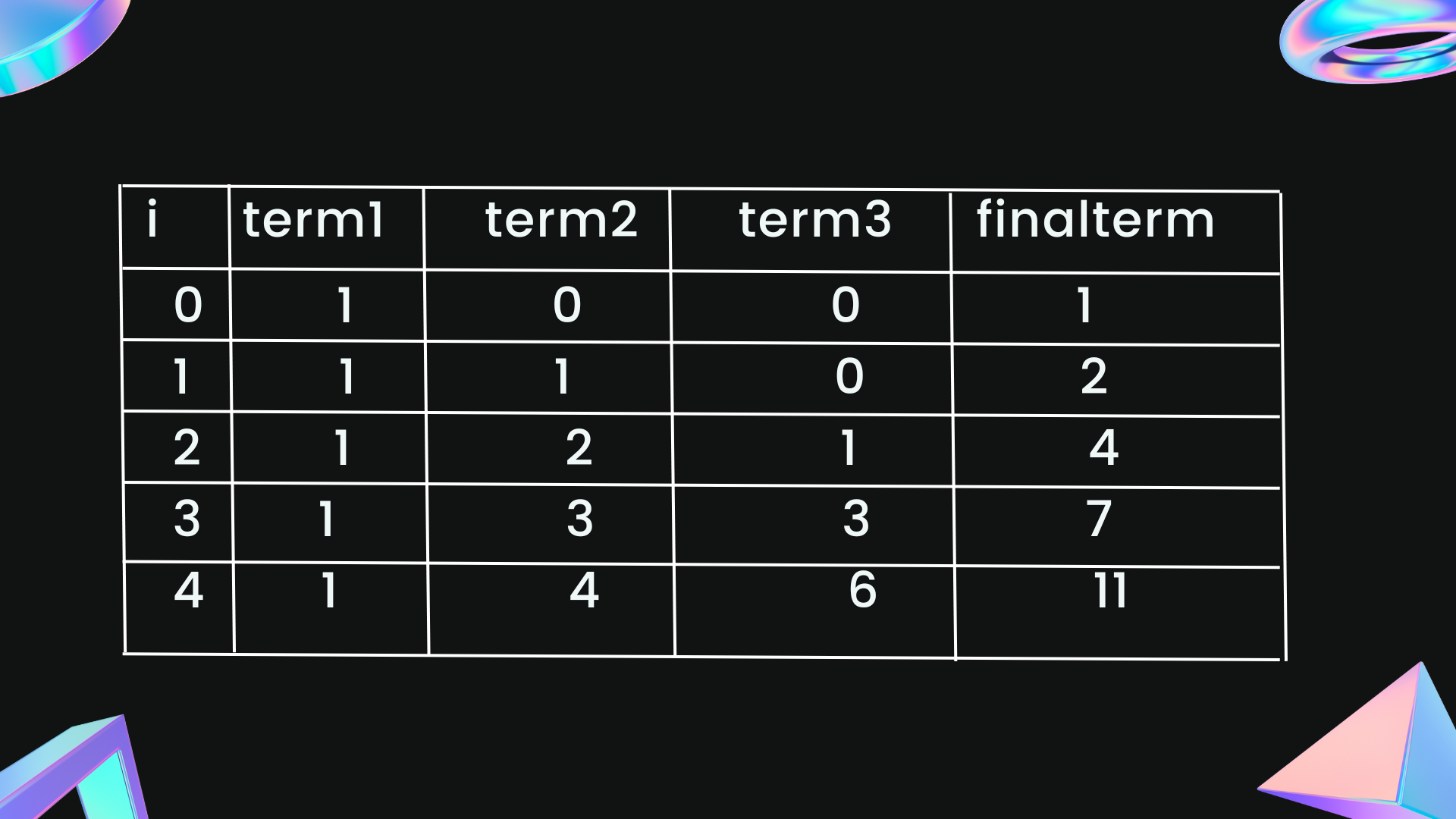
OUTPUT:
Enter the maximum number of cuts to be made : 4
The lazy caterer's sequence is...
1 2 4 7 11
METHOD-2:
In this method, the formula of (n^2+n+2)/2 will be used to calculate the terms of the lazy caterer's sequence.
VARIABLES REQUIRED:
- i- loop counter
- n-number of terms of sequence to be generated (that is the maximum number of cuts that can be made to the object)
- temp-temporary variable
ALGORITHM FOR THE MAIN FUNCTION:
- 1.Start
- 2.Accept the number of terms of the sequence to be generated in 'n'
- 3.loop counter 'i' is initialized to 0
- 4. While the loop counter 'i' is less than or equal to n , the following steps need to be repeated:
- (i)declare temporary variable temp
- (ii) calculate (n^2+n+2)/2 and store in temp
- (iii)display value of temp
- (iv)increment i by 1
- 5.Stop
PROGRAM:
#include<iostream>
using namespace std;
int main()
{
int n;
int i=0;//loop counter
cout<<"Enter the maximum number of cuts to be made:";
cin>>n;
cout<<"The lazy Caterer's Sequence is ...\n";
while(i<=n)
{
int temp=((i*i)+i+2)/2;//temporary variable
cout<<temp<<"\t";
i++;
}
return 0;
}
DRY RUN:
if n=4 then the following steps are executed in the loop: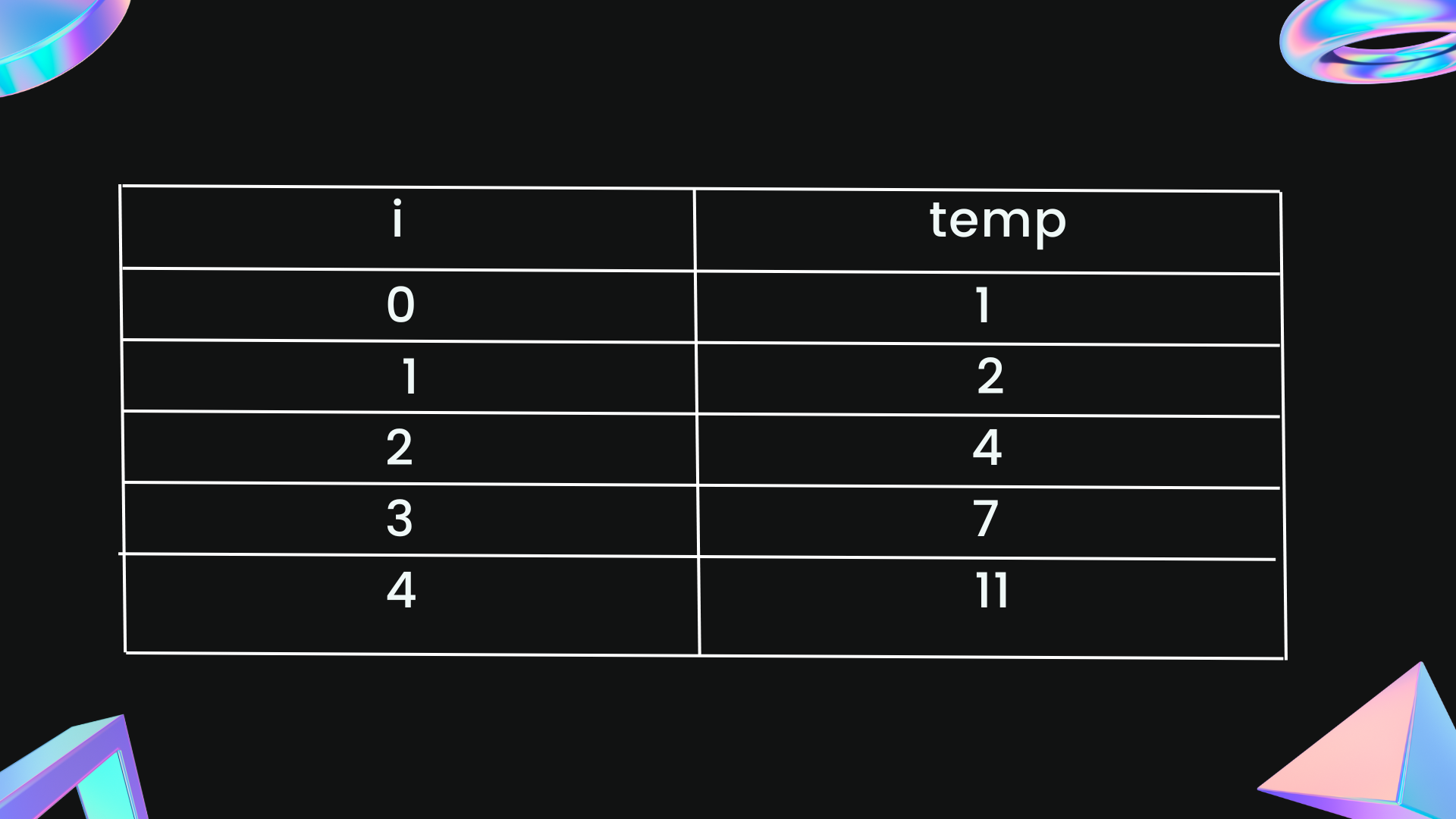
OUTPUT:
Enter the maximum number of cuts to be made : 4
The lazy caterer's sequence is...
1 2 4 7 11